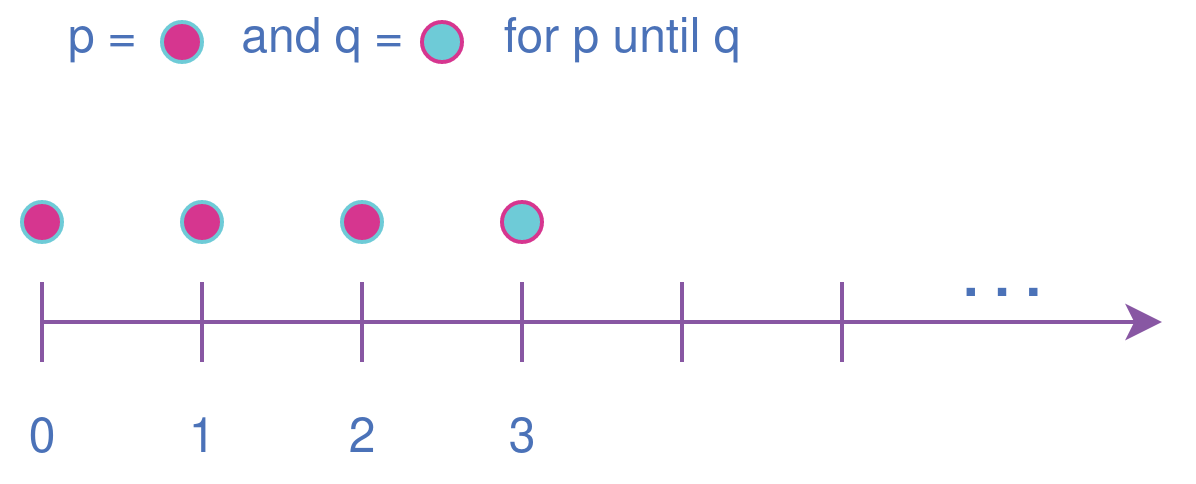Property Checking with SystemVerilog Assertions#
What You will learn in this paper |
|---|
|
Abstract#
This Application Note was written with the intention of showing a brief introduction to SVA, and is definitely not a substitute for extensive training. To learn more about formal verification and SVA, it is recommended to book the course given by the FPV specialists at YosysHQ.
Organisation#
Section Property Checking with SystemVerilog Assertions contains a brief introduction of SVA and the description of some elementary terms.
Section Assertion Types describes the different types of properties defined in the P1800, immediate and concurrent. It also presents both clock and disable conditions for concurrent assertions.
Section Elements of SVA describes each layer of SVA: Boolean, Temporal, Property and Verification layers. This section also describes some sequence property operators and property types.
Introduction#
Brief history of SystemVerilog Assertions#
Assertion Based Verification (ABV) is considered an efficient verification methodology of ASIC/SoC designs. This methodology is based on instrumenting the design with assertions that were considered in the past as executable comments that could be verified in simulation, emulation and formal property verification. These assertions served as a documentation of the design as well, being sometimes preferred over comments inlined in the RTL constructs.
Many assertion language specifications were developed to address the different verification needs with ABV. For example, ForSpec, OVA, ‘e’ and Sugar. These language specifications were not part of hardware design languages such as VHDL or Verilog mainly because they were considered as languages of different purposes.
The SVA 3.1a assertion specification was born as an integral part of the SystemVerilog specification language with the introduction of SystemVerilog 3.1a and its goals of including both hardware design and verification capabilities.
The difference between SVA 3.1a and other property specification languages is that SVA is a native part of the SystemVerilog language, and the assertions were no longer seen as interpreted comments but as part of the language itself. The standardisation of the semantics of SVA facilitated that different verification, emulation and formal property checking EDA tools could standardize its implementation, ensuring that all designs had the same results across different tools. This increased the adoption of SVA in the industry.
In SVA 3.1a, both immediate and concurrent assertions were defined as part of the standard. There were many conflicts and weaknesses in some language features that were fixed in SVA2009. Different companies have worked to improve the semantics and syntax of SVA to make it into what it is today.
The SVA (SystemVerilog Assertions) specification is part of the P1800. All the features of SystemVerilog regarding assertions are specified by the Assertions Committee (SV-AC).
Note
The SVA and PSL (Property Specification Language) are the results of different efforts that started with the standardisation of temporal logic for use in the hardware design and verification usage that Accelera Formal Verification Technical Committee started around 1998.
Introduction to SVA#
What is an assertion [1]? - From the P1800, an assertion specifies a behavior of the system. This term is confusing because is similar to the definition of property. In fact, both assert and property refer to the same thing. The inconsistency is mainly because the term assertion is adopted in ABV, and property in FPV. ABV is more widely adopted, so the term assertion is used in a more “traditionalist” way.
Note
The inconsistency in the definition of the building blocks of SVA that may lead to confusion can be read from the P1800, where assertion is defined as:
16. Assertions, 16.2 Overview, P364, Rev 2017: “An assertion specifies a behavior of the system”.
16. Assertions, 16.2 Overview, P364, Rev 2017: “An assertion appears as an assertion statement that states the verification function to be performed”.
16. Assertions, 16.2 Overview, P364, Rev 2017: “[assertion kinds …] assert, to specify the property as an obligation for the design that is to be checked to verify that the property holds”.
Whereas property, is defined as:
16.12. Declaring properties, P420, Rev 2017: “A property defines a behavior of the design”.
So in short, an assertion is an affirmation or verification construct of a behavior described using properties or the specification.
Another way to define an assertion is as an unambiguous design behavior expressed as a Boolean function or temporal expressions, that the design must fulfill. Such property are usually described using a language that can express behaviors of the design over time.
Then, what is SVA? - SVA is part of the P1800 and standardizes assertion language semantics for SystemVerilog. That standard describes the usage of a linear temporal logic [2] to define implementation correctness of a design described with properties over Boolean-valued functions and/or sequences that can be used to characterize the set of states where such formula holds, using assertions. SVA can be used for functional dynamic (simulation/emulation) and static (Formal Property Verification) testing. The focus of YosysHQ are static methods, therefore the description of SVA will be related to FPV.
Note
Although SVA talks a lot about verification tasks, it can (and should) also be used by design engineers. In fact, in FPV all properties must be synthesizable, so they are more natural for a design engineer. Using SVA instead of comments to check some functionalities of the RTL, or some behaviors when a testbench is not available, can be very useful in the RTL bring-up, for example.
The building block of SVA is the property construct, that not only distinguishes an immediate from a concurrent assertion, but is the actual element of the language where the behavior of the design is specified, for example, using Boolean functions, sequences, and other expressions. SVA introduces different kind of assertions discussed in the following sections.
Note
SVA supports both white-box and black-box verification.
Some benefits of SVA are:
Enables protocols to be specified and verified using unambiguous constructs.
Highly improves IP reuse. Interface assertions in the IP can be used as monitors for simulation/FPV to ensure correct integration.
Reduces Time to Market (TTM).
Assertions can be used instead of comments to document in a concise way design behaviors in a common and expressive language.
Among others.
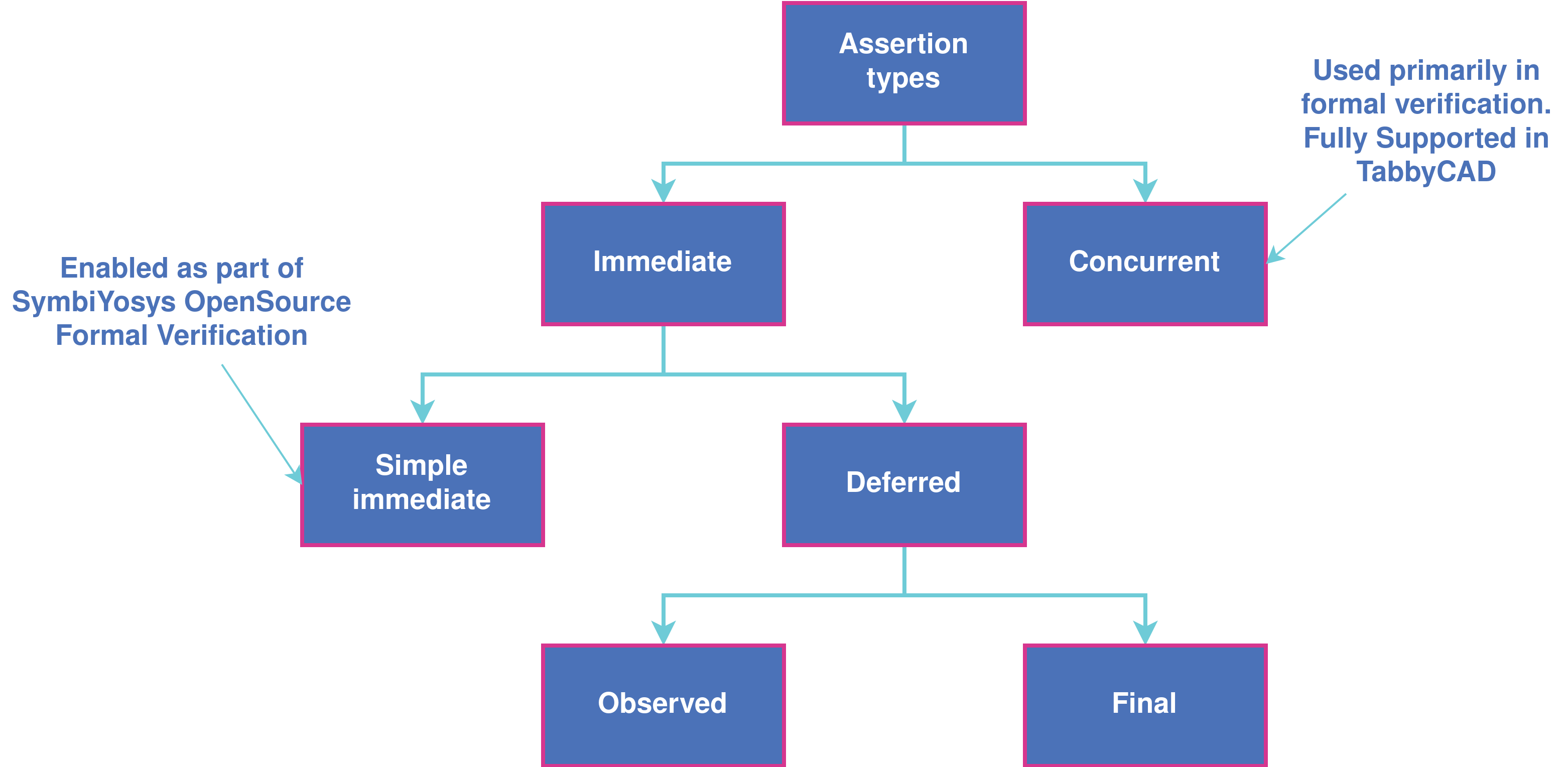
There are two kinds of assertions: immediate and concurrent. Immediate assertions are further divided into simple and deferred immediate. Deferred immediate are subdivided into observed immediate and final immediate assertions. Except from Simple immediate that are used in SymbiYosys for the open source FPV framework, and concurrent assertions, the rest are focused on simulation tasks. Immediate assertions are covered in detail in Appnote 105 Formal Property Checking Basics.
An example of a concurrent assertion is shown in Figure 3.2. This is the kind of assertion commonly using in Formal Property Verification (FPV).
As shown in Figure 3.2, the property has a verification layer with different
functions namely assert, assume,
cover and restrict that are described
in Verification Layer.
Assertion Types#
Immediate Assertions#
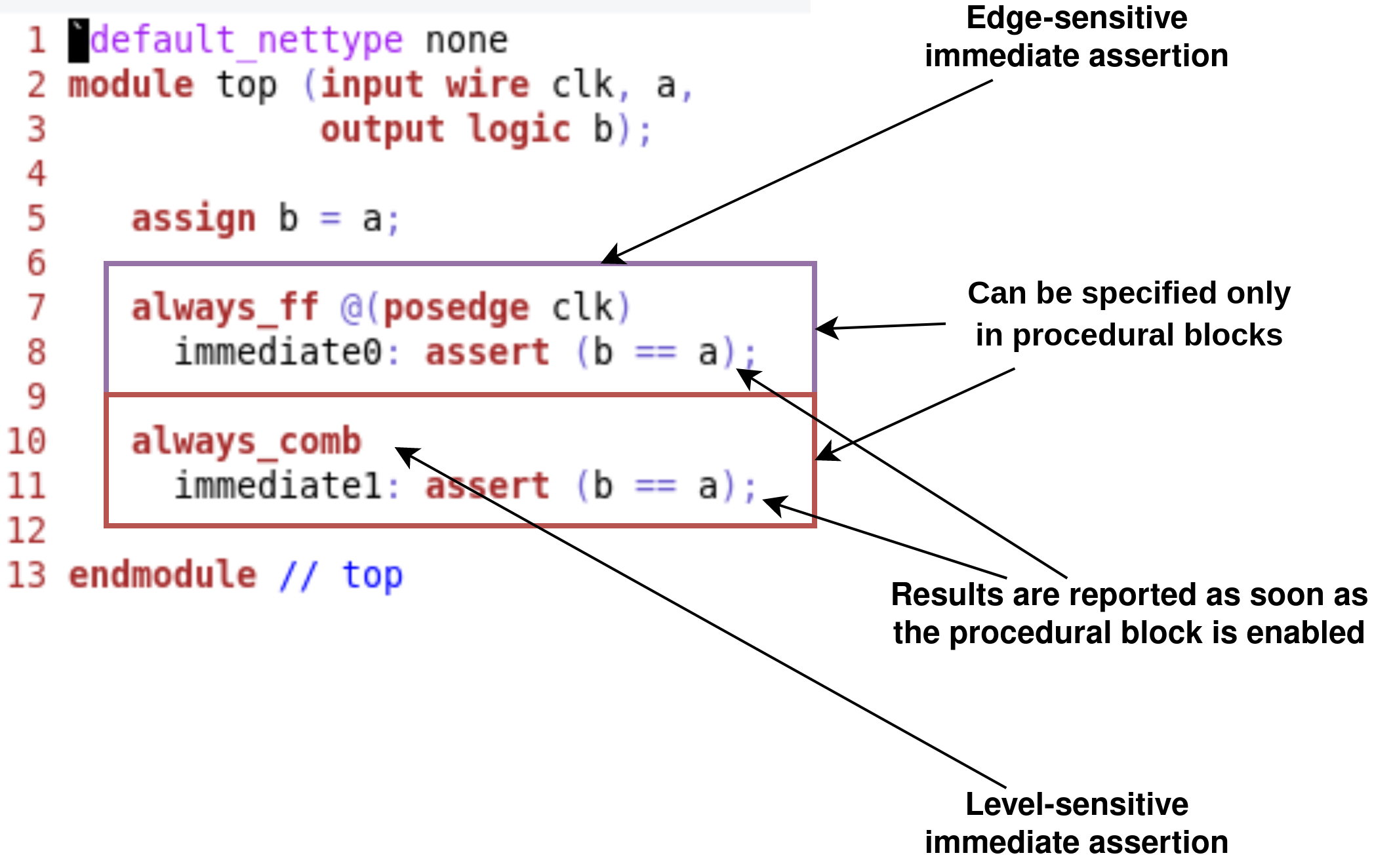
Immediate assertions are pure combinatorial elements that do not allow for temporal domain events or sequences. Immediate assertions have the following properties:
Non-temporal.
They are evaluated and reported at the same time (they cannot wait for any temporal time).
Evaluation is performed immediately.
With the values sampled at the moment of activation of the assertion condition variables.
Simpler evaluation semantics.
A clocked immediate assertion does not have the semantics of a concurrent assertion [3].
Can be specified only in procedural blocks.
Immediate assertions are better described in Appnote 105 Formal Property Checking Basics.
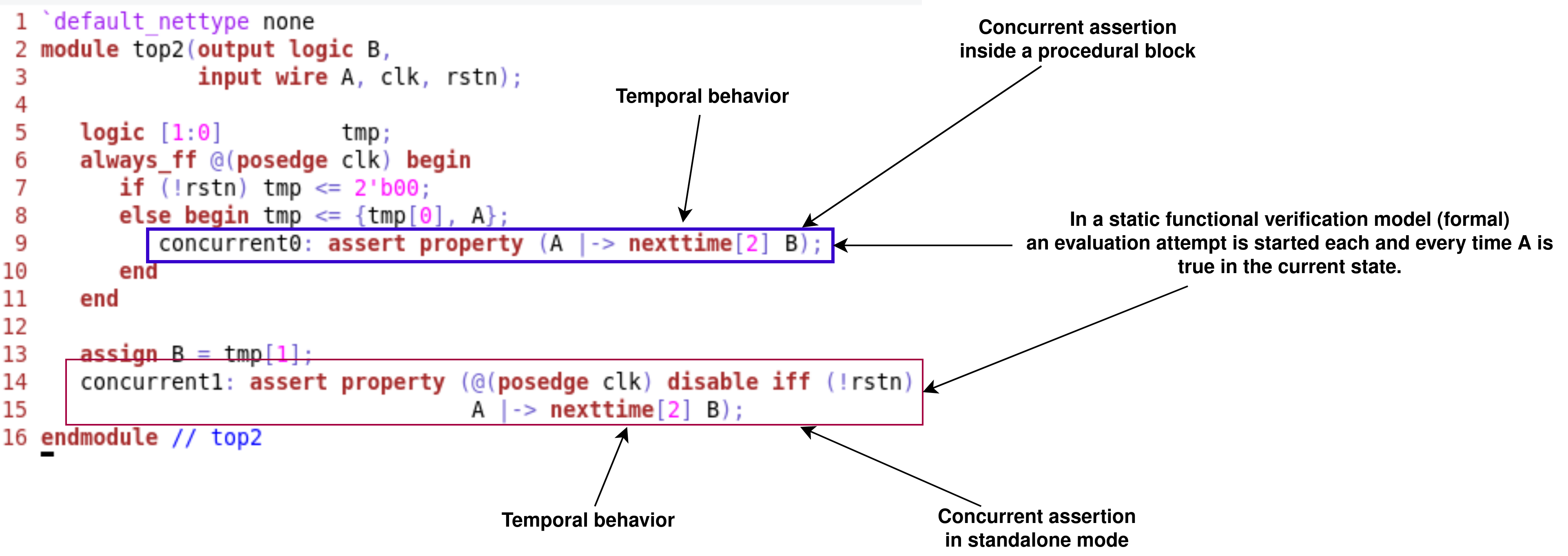
Concurrent Assertions#
The concurrent assertions capture sequences of events that span over time, that is, they have a temporal domain that is evaluated at each clock tick or time step of the system. A concurrent assertion raises the level of abstraction of SystemVerilog due the transactional nature of this construct.
Only in terms of FPV, an immediate assertion could mimic a concurrent assertion if certain helper logic is created such that it generates the notion of progress. This logic of course may not be correct and can be quite complex depending on the property expression to be described, so it needs to be verified along with the property that this logic is supposed to describe. This method is not suggested as it could add an extra verification task to the design that can be avoided using SVA.
Note
One of the advantages of the Tabby CAD Suite over the Open Source Version of SymbiYosys is that a leading-industry parser provides P1800 standard-compliant SV and SV-AC semantics for elaboration. So all the SystemVerilog constructs are enabled for the designer/validation engineers to use either for Formal Property Verification and/or FPGA synthesis.
The Figure 4.2 shows an example of a concurrent assertion definition. This kind of assertions can be defined in:
initialoralwaysblocks.Inside a systemverilog:module or systemverilog:checker object.
In a SystemVerilog
interface.For simulation, in
programblocks.
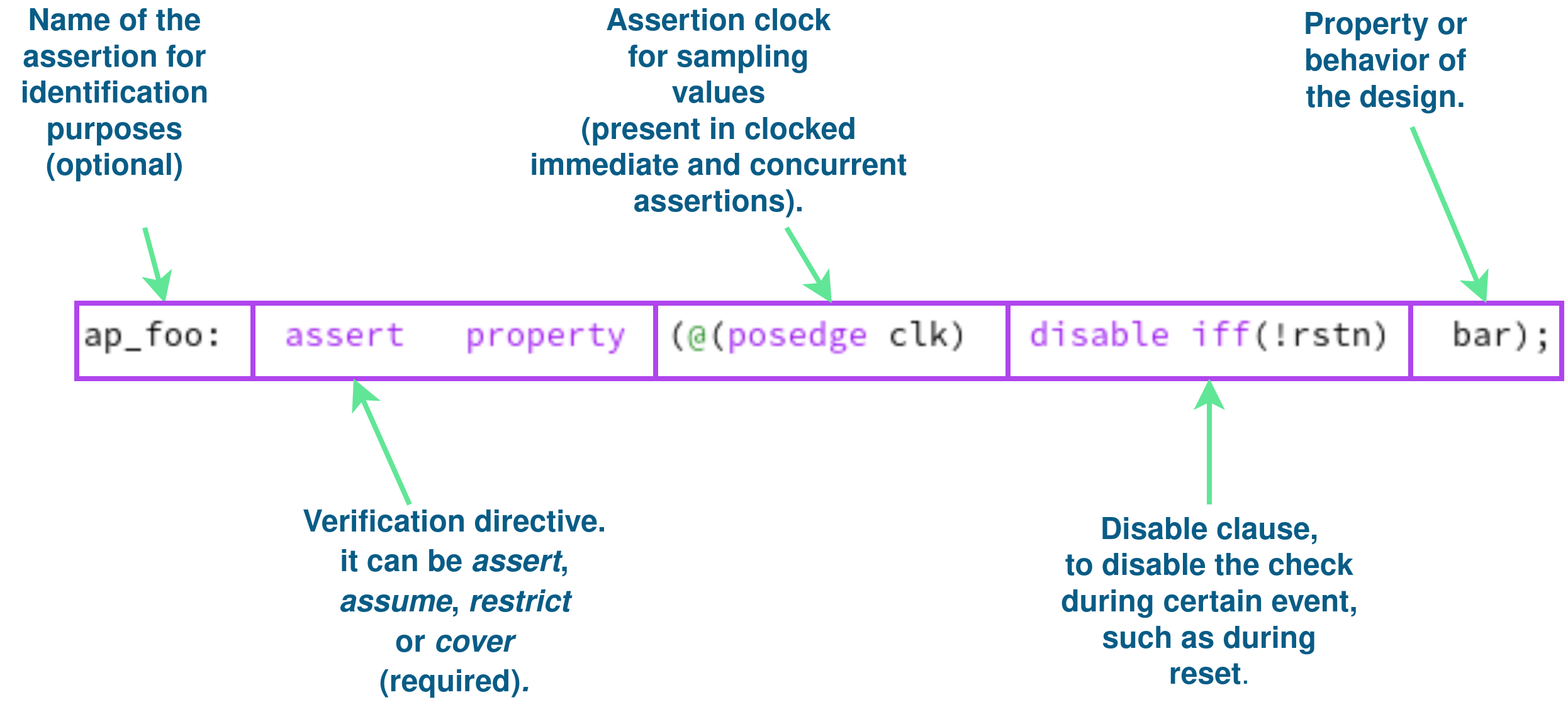
Clock or time step#
Concurrent assertions are associated with a clock which defines the sampling clock or the point in time where the assertion is evaluated. This construct helps to explicitly define the event for sampled valued functions as well, that will be discussed in next sections. The default clock event for a concurrent property can be defined using the keyword default clocking and serves as the leading clock for all the concurrent properties. The Figure 4.3 shows an example of default clocking definition.
Disable condition#
Likewise, some properties may need to be disabled during some events,
because their results are not valid anyway, for example, during the
reset state. The default disable iff (event) keywords can be used
to define when a concurrent assertion result is not intended to be
checked. The Figure 4.3 shows an example of default reset definition.
// Concurrent properties are checked each *posedge* PCLK
default clocking
formal_clock @(posedge PCLK);
endclocking
// And disabled if the *PRSTn* reset is deasserted
default disable iff (!PRSTn);
/* The property does not need to explicitly
* define PCLK as main clock and !PRSTn as disable event, as it is
* defined in the default clocking and disable blocks. */
property_a: assert property (RxStatus == 3'b011 |-> ##1
Receiver_detected);
|
|---|
Figure 4.3. Usage of default clocking and default disable events used to state that all concurrent properties are checked each posedge PCLK and disabled if the PRSTn reset is deasserted. |
Elements of SVA#
SVA Layers#
A concurrent property is composed primarily of four layers:
Boolean layer.
Temporal or Sequence layer.
Property layer.
Verification layer.
These layers makes SVA very expressive. More details are discussed in the following sections.
Boolean Layer#
Concurrent properties can contain Boolean expressions that are composed of SystemVerilog constructs with some restrictions [5]. These expressions are used to express conditions or behaviors of the design. Consider Figure 5.1 that represents the Boolean layer of a concurrent property extracted from AXI4-Stream.
// An invalid scenario that is reserved (op: not)
// occurs when there's any bit in the vector (op: wide-or)
// whose TKEEP value is LOW and TSTRB is HIGH (op: not TKEEP and TSTRB)
!(|(~TKEEP & TSTRB));
|
|---|
Figure 5.1. The Boolean layer of the following property: “A combination of TKEEP LOW and TSTRB HIGH must not be used (2.4.3 TKEEP and TSTRB combinations, p2-9, Table 2-2).” from AMBA IHI0051A. |
The evaluation of the Boolean expression shown in Figure 5.1 will be logic one when any combination of a TKEEP bit low and the same bit in TSTRB high, otherwise the result will be logic zero. The SystemVerilog Boolean operators are used in the SVA Boolean layer to represent true/false conditions.
Another type of constructs that can be expressed in the Boolean layer are the Boolean invariance properties. A Boolean invariance (or invariant) property evaluates to true on any state, in other words, a property that always holds. For example, consider the following sentence: “The packet_error port must be never asserted” that can be expressed as an assertion in the following way:
ap_never: assert property (@(posedge clk) disable iff(!rstn)
!packet_error);
The unary logical negation operator is used to express that packet_error should
not evaluate to logic one or the assertion will fail. The @(posedge clk)
implicitly implies that this Boolean condition is always evaluated, therefore this assertion
is an invariant because it should always hold.
Note
When FPV proves that an assertion holds in the design, is because the solver guarantees that the property is true in any reachable state from certain initial state. This is the definition of an invariance property, and in fact, is how the solver decides to finish the proof if he has found that the property is an invariant. This is specially helpful in certain FPV techniques to cope with complexity, such as assume-guarantee technique. Future application notes will delve into these topics.
Temporal or Sequence Layer#
The temporal layer express behaviors that can span over time, usually expressed using SERE-regular [6] expressions known as sequences that describes sequential behaviors composed of Boolean conditions that are employed to build properties.
SVA provides a set of powerful temporal operators that can be used to describe complex behaviors or conditions in different points of time.
Sequences can be promoted to sequential properties if they are used in a property context (in other words, when used in property blocks). Starting from SV09, weak and strong operators have been defined. Strong sequential properties hold if there is a non-empty match of the sequence (it must be witnessed), whereas a weak sequence holds if there is no finite prefix witnessing a no match (if the sequence never happens, the property holds).
Strong sequential properties are identified by the prefix s_ as in:
s_eventually
s_until
s_until_with
s_nexttime
Or enclosed within parenthesis after the keyword strong as in:
strong(s ##[1:$] n);
Note
The default evaluation of sequential properties (if they are weak or strong) when the weak or strong operands are omitted depends on the verification directive where they are used:
Weak when the sequence is used in assert or assume directive.
Strong in all other cases.
Some sequential property operators are discussed below.
Basic Sequence Operators Introduction#
Bounded Delay Operator#
Sequences can be more complex than just Boolean values. Basic sequences
can contain single delays (for example ##1 that means one cycle delay) and
bounded/unbounded range delays (the bounded sequence ##[1:10] means one
to ten cycles later, the unbounded sequence ##[+] means one or more
cycles later). Sequences can be enclosed within sequence {} endsequence
SVA constructs, or described directly in a property block.
A sequence can be seen as a description that defines values over time, and unlike properties or Boolean functions, a sequence does not have true or false values but matches or tight satisfaction points. For example, the sequence foo is followed by bar in one or two cycles expressed in SVA as:
foo ##[1:2] bar
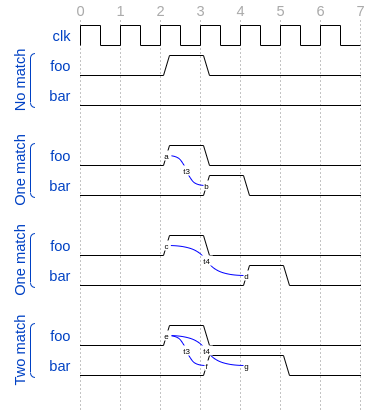
Is shown in Figure 5.2. As can be seen, there may be different match or tight satisfaction points:
When foo is true at cycle t2 and bar at cycle t3.
When foo is true at cycle t2 and bar at cycle t4.
When foo is true at cycle t2 and bar is true at cycle t3 and t4.
There is also a case where sequence does not match, which is when foo is true at cycle t2 but bar is not seen during the next one or two cycles.
The bounded operators ##m and ##[m:n] where m and n are non-negative integers, can be used to specify clock delays between two events. The Figure 5.2 is
an example of usage of these operators. For the following sequence:
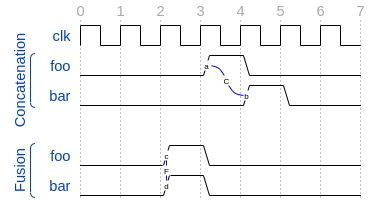
foo ##m bar
If m == 1 the sequence is split in two adjacent fragments, concatenating both foo and bar expressions. If m == 0 both foo and bar overlaps, creating a fusion of both expressions. The sequence concatenation starts matching bar in the next clock cycle after foo matches. Whereas for sequence fusion, both foo and bar start matching at the same clock tick where foo matches. See Figure 5.3 for a better understanding.
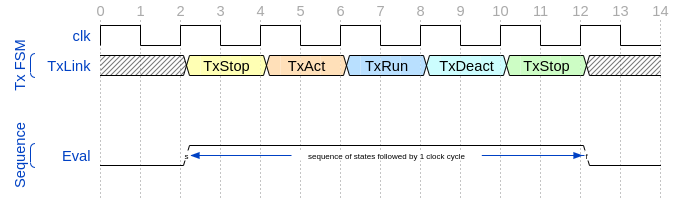
For a more concise example, consider the Figure 14-5 Combined Tx and Rx state machines from ARM IHI 0050E. To describe the transitions of the Tx Link FSM the following sequence can be defined:
/* TX FSM should transition from TxStop
* to TxAct in one to four cycles. And
* in the same way with the other states
* of the FSM, fulfilling the transitions
* shown in Figure 14-5. */
sequence tx_link_full;
fsm_lnk_ns.chi_tx_t == TxStop ##[1:4]
fsm_lnk_ns.chi_tx_t == TxAct ##[1:4]
fsm_lnk_ns.chi_tx_t == TxRun ##[1:4]
fsm_lnk_ns.chi_tx_t == TxDeact ##[1:4]
fsm_lnk_ns.chi_tx_t == TxStop ##[1:4]
endsequence
Note
The tx_link_full is a relaxed sequence because it allows the check of the transitions to happen in a small time window and not in a fixed amount of cycles. This usually helps in property convergence of complex sequences or architecture exploration for RTL development.
This sequence tx_link_full describes the transition of the Tx Link FSM from TxStop up to TxStop that precedes TxDeact. This sequence can be used in a cover or assert construct to verify that the design implements correctly the Tx Link, or to show a witness of this transition. For example, to find a trace in a design where these transitions are fulfilled, a cover construct such as the one shown below can be employed:
wp_full_tx: cover property (@(posedge ACLK) disable iff (!ARESETn) tx_link_full);
Warning
For FPV, it is always recommended to keep the cycle window small as possible since this impacts the performance of the proof.
Unbounded Delay Operator#
There are two operators for relaxed delay requirements:
Zero or more clock ticks:
##[0:$](or the shorcut##[*]).One or more clock ticks:
##[1:$](or the shorcut##[+]).
The formal semantics are the same as in the bounded delay operator. These operators are useful, for example, to check forward progress of safety properties that could be satisfied by doing nothing. What does this means?, consider the VALID/READY handshake defined in ARM IHI 0022E Page A3-9 (better known as AXI-4 specification). A potential deadlock can happen when VALID signal is asserted but READY is never asserted. If the property shown in Figure 5.4 is part of a design where READY is deasserted forever after VALID has been asserted, the property will pass vacuously.
/* , , *
* |\\\\ ////| "EXOKAY: Exclusive access okay. Indicates that *
* | \\\V/// | either the read or write portion of an exclusive *
* | |~~~| | access has been succesful". *
* | |===| | Ref: A3.4.4 Read and write response structure, *
* | |A | | pA3-57, Table A3-4. *
* | | X | | *
* \ | I| / *
* \|===|/ *
* '---' */
property rdwr_response_exokay (valid, ready, resp);
(valid && ready &&
(resp == amba_axi4_protocol_checker_pkg::EXOKAY));
endproperty // rdwr_response_exokay
|
|---|
Figure 5.4. A property that monitors the EXOKAY response value when VALID and READY are asserted. |
To check that the system is actually making progress, the property using one or more clock ticks operator shown in Figure 5.5 can be used. If this property fails, then the FPV user can deduce that property of Figure 5.4 is not healthy.
// Deadlock (ARM Recommended)
/* , , *
* |\\\\ ////| It is recommended that READY is asserted within *
* | \\\V/// | MAXWAITS cycles of VALID being asserted. *
* | |~~~| | This is a *potential deadlock check* that can be *
* | |===| | implemented as well using the strong eventually *
* | |A | | operator (if the required bound is too large to be *
* | | X | | formally efficient). Otherwise this bounded *
* \ | I| / property works fine. *
* \|===|/ *
* '---' */
property handshake_max_wait(valid, ready, timeout);
valid & !ready |-> ##[1:timeout] ready;
endproperty // handshake_max_wait
|
|---|
Figure 5.5. A property that checks for a deadlock condition. If VALID is asserted and READY is not asserted in timeout non-negative cycles, the property will be unsuccessful. |
Note
The property of Figure 5.5 can still fail in certain scenarios. This is because the unbounded operator employed in the property definition has weak semantics. A better solution could be to make this property strong but this implies that this safety property will be converted into a liveness one. Liveness and safety concepts are described in Property Layer section.
Consecutive Repetition#
Imagine the following property from an SDRAM controller (JESDEC 21-C): The WR (write) command can be followed by a PRE (precharge) command in a minimum of tWR cycles. If tWR == 15 then the property can be described as follows:
let CMDWR = (cmd == WR && bank == nd_bank);
let notCMDPRE = !(cmd == PRE && bank == nd_bank);
// notCMDPRE must hold 15 times after WR command is seen
property cmdWR_to_cmdPRE;
CMDWR |-> ##1 notCMDPRE ##1 notCMDPRE ##1 notCMDPRE
##1 notCMDPRE ##1 notCMDPRE ##1 notCMDPRE
... ##1 notCMDPRE ##1 notCMDPRE;
endproperty
Note
The let declaration serves as customization and can be used as a replacement for text macros, but with a local scope. Also, unlike the compiler directives ifdef, ifndef, etc, the let construct is part of the SystemVerilog language, so it is safer to use than macros.
This is too verbose and not an elegant solution. SVA has a construct to define that
an expression must hold for m consecutive cycles: the consecutive repetition
operator [*m]. The same property can be described using the consecutive
repetition operator as follows [7]:
let CMDWR = (cmd == WR && bank == nd_bank);
let notCMDPRE = !(cmd == PRE && bank == nd_bank);
// notCMDPRE must hold 15 times after WR command is seen
property cmdWR_to_cmdPRE;
CMDWR |-> ##1 notCMDPRE [*15];
endproperty
And if the tWR value is set as a parameter, then this can be further reduced to:
CMDWR |-> ##1 notCMDPRE [*tWR];
As with delay operators, sequence repetition constructs have some variants such as:
Consecutive repetition range
s[*m:n]: The sequence s occurs from m to n times.Infinite repetition range
s[*]: The sequence s is repeated zero or more times.Infinite repetition range
s[+]: The sequence s is repeated one or more times.Nonconsecutive repetition operator
s[=m:n]: The sequence s occurs exactly from n to m times and s is not required to be the last element.GoTo repetition operator
s[->m:n]: The sequence s occurs exactly from n to m times and s is required to be the last element.
Warning
Not all sequential property operators are FPV friendly:
GoTo and nonconsecutive operators.
Throughout.
Intersect.
first_match().
Within.
Etc.
These operators increases the complexity of the model and may cause some assertions not converge. Use them with caution.
All these operators was demonstrated in practice using the same seq.sv in the past, by Matt Venn, so they will not be shown again in this document. The reader is invited to generate some random sequences and try the operators in some properties. It is a great exercise to understand the fundamentals of sequential properties.
Property Layer#
The property layer is where all the expressiveness of SVA starts to take shape. In
this layer, Boolean constructs, sequences and property operators are used to
encapsulate the behavior of the design within property ... endproperty blocks
that will be further utilised by the verification layer to perform a certain task.
A property construct can have formal arguments as shown in Figure 5.4 and Figure 5.5, that are expanded when the property is instantiated with the proper arguments. Properties can also have no arguments.
The P1800 defines several kinds of properties of which some are shown below:
Sequence: As described in Section Temporal or Sequence Layer, a sequence property have three forms namely sequence_expression, weak(sequence_expression) and strong(sequence_expression). Remember that a sequence is promoted to a sequence property if the sequence expression is used in property context.
Negation: This property uses the not property_expression operator to basically evaluate to true if property_expression is false.
Disjunction: A property of the form property_expression1 or property_expression2 evaluates to true if at least one of the property expressions evaluates to true.
Conjunction: A property of the form property_expression1 and property_expression2 evaluates to true if the two property expressions evaluates to true.
If-else: This property has the form if (condition) property_expression1 else property_expression2 and can be seen as a mechanism to select a valid property based on a certain condition.
Implication: One of the most used kinds of properties in ABV. This property has the form sequence_expression |=> or |-> property_expression that connects the cause (expression in LHS or antecedent) to an effect (expression in RHS or consequent). More about this type of property is described in YosysHQ AppNote 120 – Weak precondition cover and witness for SVA properties.
The rest of the kinds of properties are better explained with a graph as shown below.
Note
There are different versions of the following properties. Refer to P1800 (2017) Section 16.12 Declaring properties for more information.
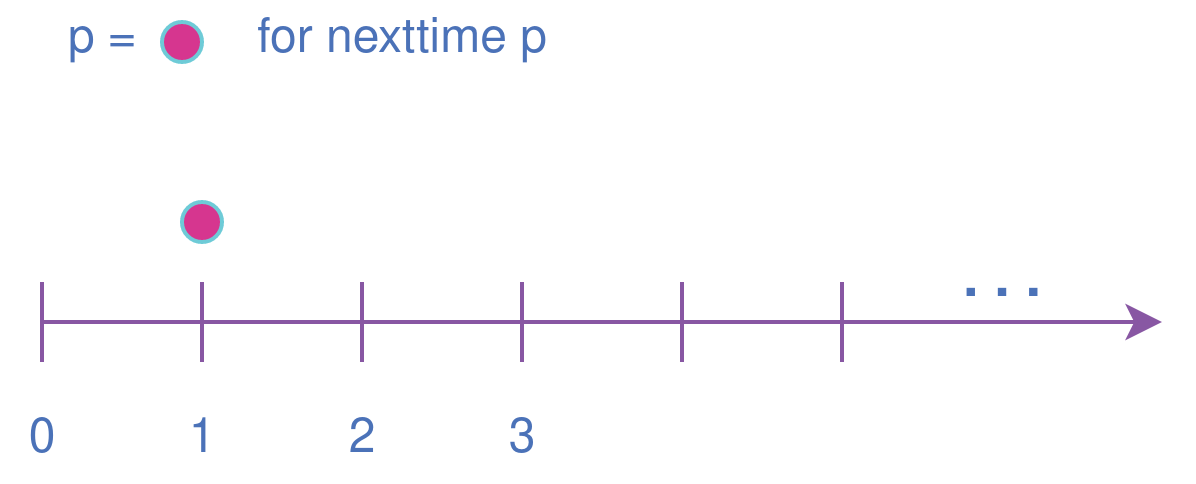
Nexttime property This property evaluates to true if the property expression p is true in the next clock cycle.
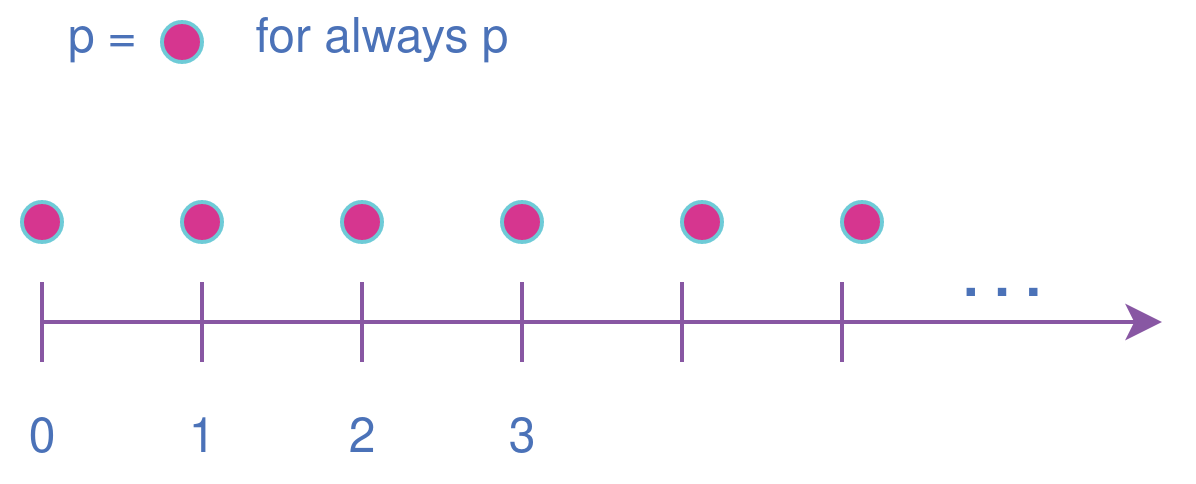
Always property This property evaluates to true if the expression p holds at all states.
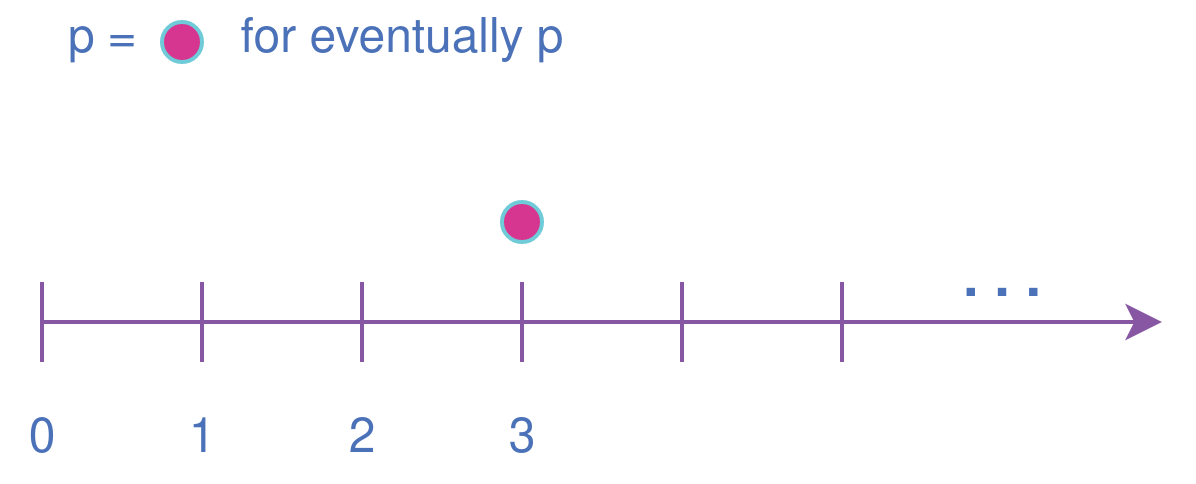
Eventually property This property evaluates to true if the expression p holds at some time in the future.
Until property The property p until q is true starting from an initial point if q is true in some reachable state from the initial state, and p is true in all states until q is asserted.
Safety Properties#
A safety property, in short, checks that something bad never happens. It is the most used type of property in FPV because it is less complicated for a solver to find a proof, compared to the liveness case (for example, by proving inductively that the property is an invariant).
These might be the results of a safety property:
A full proof is reached, meaning that the solver can guarantee that a “bad thing” can never happen.
A bounded proof showing that the “bad thing” cannot happen in a certain number of cycles.
A counterexample of finite prefix showing the path where the “bad thing” happens.
An example of a safety property extracted from IHI0051A amba4 axi4 stream is shown below:
/* , , *
* |\\\\ ////| "Once TVALID is asserted it must remain asserted *
* | \\\V/// | until the handshake (TVALID) occurs". *
* | |~~~| | Ref: 2.2.1. Handshake Protocol, p2-3. *
* | |===| | *
* | |A | | *
* | | X | | *
* \ | I| / *
* \|===|/ *
* '---' */
property tvalid_tready_handshake;
@(posedge ACLK) disable iff (!ARESETn)
TVALID && !TREADY |-> ##1 TVALID;
endproperty // tvalid_tready_handshake
|
|---|
Figure 5.10. A safety property to state that a packet should not be dropped if the receiver cannot process it. |
Liveness Properties#
A liveness property checks that something good eventually happens. These kinds of properties are more complex to check in FPV because in contrast to safety properties a CEX cannot be found in a single state. To find a CEX, sufficient evidence is needed that the “good thing” could be postponed forever, and sometimes an auxiliary property is needed to help the solver understand that there is some progress ongoing (fairness assumption).
A safety property can be trivially proven by doing nothing, because this will never lead to a scenario where a “bad thing” occurs. A liveness property complements safety properties, but they are more difficult to prove because the solver needs to guarantee that something will happen infinitely many times.
An example of a liveness property is from the classic arbiter problem that states that every request must be eventually granted, that can be described in SVA as follows:
property liveness_obligation_arbiter;
req |=> s_eventually gnt
endproperty
Another example of a liveness property that defines that a handshake must eventually occur between a sender and a receiver, from the IHI0022E AMBA and AXI protocol spec, is shown below.
// Deadlock (ARM Recommended)
/* , , *
* |\\\\ ////| It is recommended that READY is asserted within *
* | \\\V/// | MAXWAITS cycles of VALID being asserted. *
* | |~~~| | This is a *potential deadlock check* that can be *
* | |===| | implemented as well using the strong eventually *
* | |A | | operator (if the required bound is too large to be *
* | | X | | formally efficient). Otherwise this bounded *
* \ | I| / property works fine. *
* \|===|/ *
* '---' */
property handshake_max_wait(valid, ready);
valid & !ready |-> strong(##[1:$]) ready;
endproperty // handshake_max_wait
|
|---|
Figure 5.11. Using a liveness property to check for deadlock conditions. This is a very common practice. |
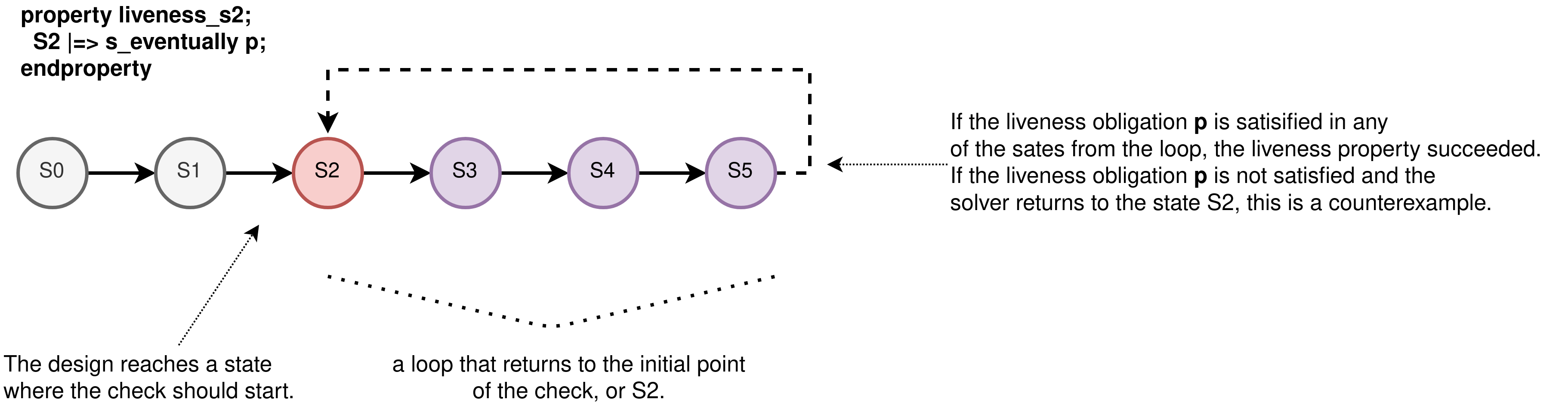
A deep explanation of how a solver of a FPV tool finds a liveness CEX is outside of the scope of this application note, but for the sake of clarity, consider Figure 5.12 that explains in broad terms the rationale behind liveness property analysis.
Verification Layer#
A property by himself does not execute any check unless is instantiated with a verification statement. In section Property Layer results of property evaluation are constantly mentioned. Those values and conditions applies when the property is used with the verification directives listed below:
Note
For simulation, properties works as monitors that checks the traffic/behavior of the test vectors applied to the design under test. For FPV, properties are non-deterministic since all possible values are used to check a proof.
assert: Specifies validity, correctness, or a behavior that a system or design is obligated to implement. When using the assert function, the solver’s task is to either conclude that the assertion and the design are a tautology or to show a counterexample (CEX) indicating how the design violates or contradicts the assertion. Behaviors are observed on the outputs of a Boolean functions, either design primary outputs or internal signals where some calculations of interest happens. In short, The assertion w.r.t of a property must be true for all legal values applied at design inputs.
assume: The property models how inputs of the design are driven in an unexamined way, that is, as a fact that the solver does not check but uses to constrain the valid values that will be used in the primary inputs. when an assertion with related input assumptions is proven, it is said that it holds assuming only the values constrained at the input are driven in the block under test. Modeling assumptions is one of the most error-prone tasks in formal verification that can cause some problems such as vacuity as described in YosysHQ AppNote 120 – Weak precondition cover and witness for SVA properties. Assumption correctness is not checked by the formal tool.
cover: Checks for satisfiability, that is, an evidence of whether any given behavior is implemented in the design. The main difference with the assertion statement is that when using the cover statement on a property, the proof succeed if there is any behavior in the design that the property dictates. For the proof under assertion directive, the behavior should be observed for all conditions in the inputs of the design.
restrict: This directive is primarily used in FPV and is ignored in simulation. The restrict directive has similar semantics as assume, but is intended to use as delimiter in the state space, or in other words, to help in assertion convergence [4]. For example, the restrict verification directive can be used to prove in a separated way, each arithmetic opcode (such as add, sub, etc). If the same environment is reused in simulation, the simulator will ignore the restriction. Otherwise, if an assumption had been used, the simulator would have failed because it cannot be guaranteed that certain opcode is the only one applied to the design.
For example, to assert the deadlock-free property shown in Figure 5.5, the following construct can now be defined using all the SVA layers:
ap_AW_SRC_DST_READY_MAXWAIT:
assert property(disable iff (!ARESETn) handshake_max_wait(AWVALID, AWREADY))
else $error("Violation: AWREADY should be asserted within MAXWAIT cycles",
" of AWVALID being asserted (AMBA recommended).");
|
|---|
Figure 5.13. Using the AXI deadlock property as an assertion. |
In this way and using the other verification directives as well, FPV users can create powerful SVA checks for simple and complex designs.
Note
The action block (or the `else $error [...]) is not synthesizable, therefore
an FPV tool will not execute that part of the assertion. This helps to debug
the case where a property is failing as the FPV user can see the source code and get
an idea of where to check for more information.
It is also important to give a meaningful name to all the properties/assertions,
so debugging and readability are improved. If no name is given to a property,
the FPV tool will assign a name to it.
More Advanced SVA Constructs#
Checkers#
Usually, properties are defined inside a module but this has been proven to be a problem in certain scenarios. For example, in a module, all port types must be explicitly defined but to reuse properties sometimes it is needed that the unit that encapsulates the SVA constructs can admit any type as input (to make it generic). Also, modules cannot accept sequences and/or properties as inputs and some other drawbacks that the construct checker … endchecker solves.
For example, a checker to create the deadlock-free checker for property shown in Figure 5.11 the following code can be used:
checker deadlock_axi(sequence handshake_start, property handshake_end);
default clocking fpv_clk @(posedge ACLK); endclocking
default disable iff(!ARESETn);
property handshake_max_wait(valid_seq, ready);
valid_seq |=> s_eventually ready;
endproperty // handshake_max_wait
deadlock_free: assert property(handshake_max_wait(handshake_start, handshake_end));
endchecker
SystemVerilog System Functions in SVA#
The P1800 provides some system functions and utilities that can be used to increase expressibility of SVA, these are the Bit Vector Functions and Sampled Value Functions. System functions are well described in the P1800 LRM and are quite straightforward to understand. Some examples are shown below for the sake of exemplification. These examples contains some errors that needs to be fixed.
Note
To use SystemVerilog system functions, the argument of the function must be known at elaboration time. Remember that all components of SVA for FPV must be synthesizable.
Bit Vector Functions Reference#
The $countbits function#
This function returns the number of bits of an specific set of values in a bit vector. See the following example.
seq #("__________________-_") seq_a(clk, a); ap_countbits: assert property($countbits(a, '1) == 1'b0);
Execute sby -f ./src/src/system_functions/systemf_bv.sby err and see the result, it may need to be fixed.
The $countones function#
Counts the number of 1’s in a bus, equivalent to $countbits(expr,'1).
See the following example.
seq #("__________________-_") seq_a(clk, a); ap_countones: assert property($countones(a) == 1'b0);
Execute sby -f ./src/src/system_functions/systemf_bv.sby err and see the result, it may need to be fixed.
The $onehot0 function#
Evaluates to true if at most one bit of the bus is set to logic one, otherwise it evaluates
to zero. As its name mentions, it is used to check that some bits are mutually exclusive. This
expression is equivalent to $countbits(expression,'1)<=1. See the following example:
seq #("00000000000000000000", 2) seq_b(clk, b); ap_onehot0: assert property($onehot0(b));
Execute sby -f ./src/src/system_functions/systemf_bv.sby err and see the result, it may need to be fixed.
The $onehot function#
It is similar to $onehot0 with the difference that $onehot
is equivalent to $countbits(expression,'1)==1 (exactly one bit set to
logic one) and $onehot0 requires at most one (or none) bits set to 1. See
the following example:
seq #("00000000000000000000", 2) seq_b(clk, b); ap_onehot: assert property($onehot(b));
Execute sby -f ./src/src/system_functions/systemf_bv.sby err and see the result, it may need to be fixed.
The $isunknown function#
This function evaluates to true if any bit from the vector has a don’t care (‘x) or high impedance (‘z). At the moment, Tabby CAD has some limitations on these data types so the example will be skipped. This function can be used in FPV to debug and detect X-propagation in digital designs.
Sampled Value Functions#
The $sampled function#
This function simply returns the sampled value of the argument. This function is
redundant for concurrent assertions and FPV [8], and is more useful in simulation.
However, there exist a case where is useful for FPV: when using disable iff(reset) to define when the check is disabled, this reset results in an
asynchronous event (i.e., the check will be disabled at any time reset becomes 1).
Using the $sampled function the disable condition can be “synchronized”:
assert property (@(posedge clk) disable iff($sampled(reset)) p |-> q);
The $past function#
This system function has been studied frequently in other SymbiYosys tutorials. It simply returns the sampled value of the expression in n steps ago. The value of the expression before the initial clock may be undefined, causing the property to fail.
// If a is true in the current clock cycle it must be true // in the previous cycle as well. seq #("_-------------------") seq_a(clk, a); ap_past: assert property($past(a));
Execute sby -f ./src/src/system_functions/systemf_sv.sby err and see the result, it may need to be fixed.
The $rose function#
This function returns true if the LSB of the expression was 0 in the previous clock tick and 1 in the current.
// If b becomes 1, it must be 1 for the next 5 clock cycles seq #("-------____________-") seq_b(clk, b); ap_rose: assert property($rose(b) |=> b[*4]); cp_rose: cover property($rose(b) ##1 b[*4]);
Execute sby -f ./src/src/system_functions/systemf_sv.sby err and see the result, then run sby -f ./src/src/system_functions/systemf_sv.sby cover and compare the result. It may need to be fixed.
The $fell function#
This function returns true if the LSB of the expression was 1 in the previous clock tick and 0 in the current.
// If c becomes low, it must be low for the next 5 clock cycles seq #("------------------__") seq_c(clk, c); ap_fell: assert property($fell(c) |=> c[*4]); cp_fell: cover property($fell(c) ##1 c[*4]);
Execute sby -f ./src/src/system_functions/systemf_sv.sby err and see the result, then run sby -f ./src/src/system_functions/systemf_sv.sby cover and compare the result. It may need to be fixed.
The $changed function#
Returns true if the logic value of the expression changed.
// d toggles forever seq #("_-_-_-_-_-_-_-_-_-_-") seq_d(clk, d); ap_changed: assert property(<implement the assertion>);
Write the property ap_changed and run sby -f ./src/src/system_functions/systemf_sv.sby, then try to get a witness of this property.
The $stable function#
Returns true if the logic value of the expression remains stable, as seen in Consecutive Repetition.
References#
The YosysHQ AppNote 109 repository: https://github.com/YosysHQ-Docs/AppNote-109
1800-2017 - IEEE Standard for SystemVerilog Unified Hardware Design, Specification, and Verification Language.
Bustan, D., Korchemny, D., Seligman, E., & Yang, J. (2012). SystemVerilog Assertions: Past, present, and future SVA standardization experience. IEEE Design & Test of Computers, 29(2), 23-31.
The AMBA AXI4 Stream SVA Verification IP for FPV which was used to show some of the properties described in this AppNote can be obtained in: https://github.com/dh73/A_Formal_Tale_Chapter_I_AMBA